Ultimate Guide to LSAT Ordering Game Diagrams

If you’re prepping to take the LSAT, then you’re probably already aware that one of the biggest challenges ahead is learning to tackle the LSAT logic games. When you first start studying for LSAT logic games—which on the official test are called “Analytical Reasoning” questions—they can seem totally unpredictable and impossible to study for.

However, when you spend enough time with different LSAT logic game explanations, you might realize that the vast majority of LSAT logic games can be broken down into a few different types of games. This is one of the benefits of working with an LSAT logic game tutor. LSAT logic game tutoring can help you learn the most powerful strategies for tackling virtually any LSAT logic game.

The most common and most basic form of LSAT logic game is the sequencing game—sometimes called the ordering game. And that’s the one we’re going to cover in this post.

Here we’ll present you with a sample sequencing game, and we’ll walk you through the steps necessary to make sense of it and to answer all the questions accurately. 

Don’t Do It In Your Head

The LSAT is such a wordy exam, and the logic games are all presented as written information. This often leads students to try to work out the answers in their head. However, this is a huge mistake. It’s virtually impossible to hold all the information provided in your head. If you try to work out the answers that way, you’re all but guaranteed to jumble information and leave yourself confused. 

Draw a Main Diagram

The best way to start with an LSAT logic game is to draw a main diagram. This main diagram will represent all the information and rules provided for that particular game, providing you with a visual reference to help you answer the questions, so you don’t have to work everything out mentally. For many of the questions, you may have to draw sub-diagrams, but an effective and clear main diagram will save you a lot of time.

Work Out the Variables

Standard LSAT sequencing games contain two different types of variables, which we might call the slots and the elements. The slots are fixed, and the elements are the moveable pieces that go into those slots in a particular order based on the information provided. The first thing to do is work out which of the variables involved represent the slots and which represent the movable elements.

Let’s use a sample LSAT logic game and the logic game explanation for the rest of this article. 

A bus driver is set to stop at six destinations—Ableton, Brownsville, Clarkmore, Danton, Edwardia, and Farm City. The bus only stops at each destination once. 

In this prompt, the two sets of variables are the order of stops and the different destinations. Obviously, the order of stops—first through sixth—is unchanging. It’s the destinations that change. Therefore, the order of stops will serve as the base of your diagram. Setting up your base is always the best way to start with your LSAT logic game strategy.  

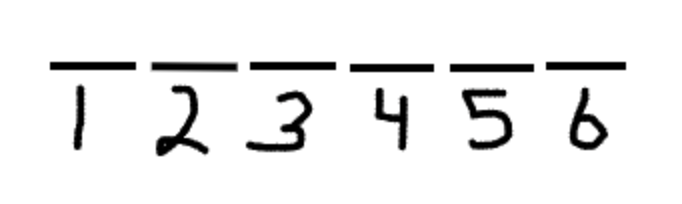
The other variables—the destinations—should be abbreviated to just their initials and placed at the top left of your diagram. This will serve as a bank that you can refer to as you implement the various rules of the game and try to figure out which destination goes in which slot in the order. 

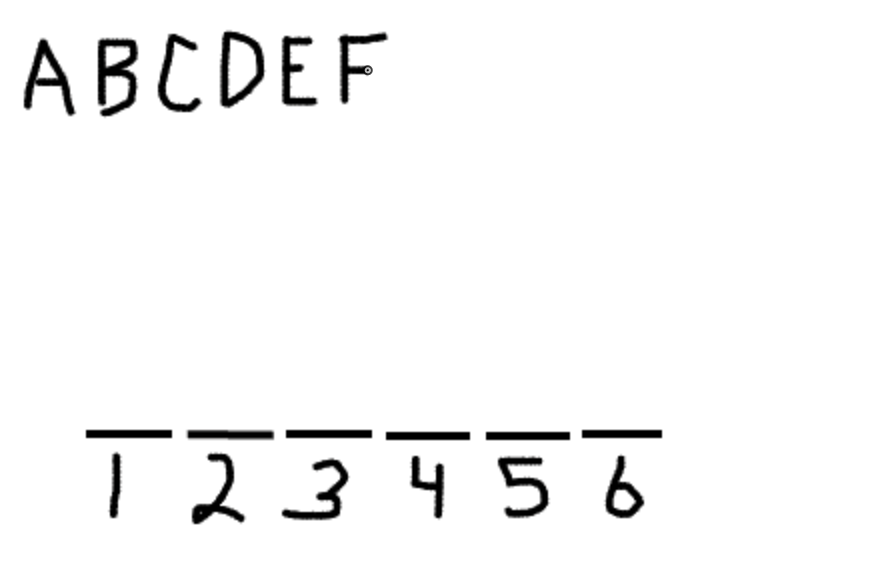
Notice that we didn’t abbreviate Farm City to FC. Just abbreviating it to F keeps things simpler. If we’d made it FC, then we might have confused it for a combination of two destinations—F and C. Abbreviating the elements to single initials helps us keep from getting distracted by unnecessary details. It also helps us to interiorize the fact that, once you strip away the details, all LSAT sequencing/ordering games are virtually the same. 

After Sketching Your Main Diagram, Add the Rules

It’s not just the variables in an LSAT logic game that can be abbreviated and inserted into your diagram—you can visually represent the rules also. Different testing and prep companies may have slightly different systems for how to represent the rules, but they’re mostly pretty similar. You can experiment with them if you find a strategy that seems to work better with your thinking style. 

Okay, now let’s take a look at the rules for this game:

The bus stops in Brownsville after stopping in Clarkmore.

The bus stops in Farm City after stopping in Danton.

The Danton stop comes exactly three stops after the stop in Ableton.

The Clarkmore stop is either first or third. 

The first rule is a good example of the most classic and common type of rule you’ll find in LSAT ordering games. It’s very simple. So now we’re going to represent that visually in a way we can easily refer back to, understand, and make efficient use of as we move forward.

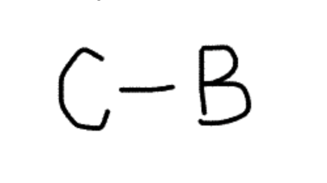
That’s it. Pretty simple, right? You could also use an arrow instead of a dash, if you’d like, or a greater-than symbol. One thing that you should take note of about this form of representation is what it doesn’t mean. It doesn’t mean that C comes immediately before B, because the rule doesn’t say that explicitly. It just means that it comes at some point before B. If the rule told is it came immediately before B, we would want to find a different way of representing that rule…perhaps by drawing two consecutive slots with a box around them indicating that they go together in a unit. We’ll deal with some rules like that in a bit. 

Now let’s look at the second rule, which can be rewritten as: “F comes before D.” This is basically the same kind of rule as the first, so we’ll write it in the same way.

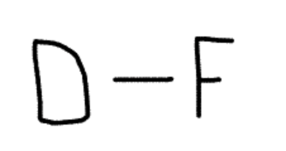
The third rule is a bit different. While the first two rules simply a before/after order without any specificity as to the range of slots between the elements, the third rule is much more specific about how many slots it’s dealing with. We learn there are exactly two slots between A and D. Therefore, we want to represent that visually in a way that will help us, so when we refer to it, we know exactly what we’re dealing with.

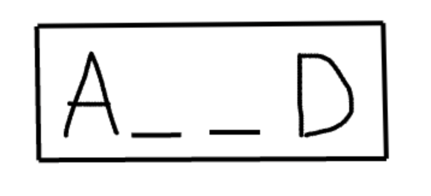
The two blank slots and the box around the whole set shows us that this is a specifically bounded rule. It’s showing us a set of four elements—two of which are known—which goes in a specific order. This will help us remember exactly how this rule is operating, and it will help our visual brain as we try to sort these elements. Wherever A goes, there are two unspecified slots after it, followed by D. Conversely, wherever D goes, there are two unspecified slots before it, with A before that. We don’t currently know which elements go in those two slots, but we still gain a lot of information. We can also see that D, therefore, cannot go any earlier than fourth in the whole sequence. Further, A cannot go any later than third, otherwise this block would not fit in our diagram.

Let’s take a brief detour to look at some other kinds of rules that might be appropriate for using blocks. 

Let’s say we had a rule that said something like: J goes immediately before or after K. We don’t know which goes first, but we know they’re connected. In that case, a block will help us remember. There are two effective ways we can represent this. 

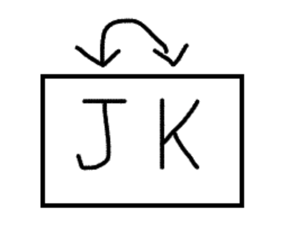
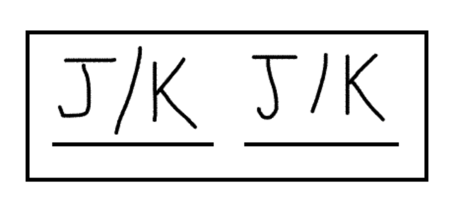
The first uses a bidirectional arrow to represent that the order we’ve written the elements in can be reversed. Another puts both elements, J and K, in consecutive slots, with a slash indicating that either can go in either slot. But the block around these elements keeps us from forgetting that they will inevitably be connected, with one coming right before or right after the other, and no other elements in between.

We might also get a slightly more complicated rule that says something like: There is exactly one stop between J and K. This is kind of a combination of the different rules we’ve dealt with so far, but now we have the skills to represent it in a way that makes sense. In this case, what we do is we draw a block that contains three slots. Then we write J/K in the first and the third slots. This shows us that we don’t know whether J or K comes first or third, but we know that they have an unspecified stop between them.

Some Rules Go Straight Into Your Diagram

When working toward an LSAT logic game solution, we should always be on the lookout for rules that we can apply directly to our main diagram. This will help us keep all the relevant information front of mind as we try to figure out where all the different elements go. 

We can do this with the fourth rule, which says that Clarkmore is either the first or third slot. Generally speaking, whenever a rule in an ordering game gives you specific information about which slots might be involved—as opposed to just general guidelines about the relationships between the movable variables—it can go into your main diagram. Here’s an effective way of representing that rule.

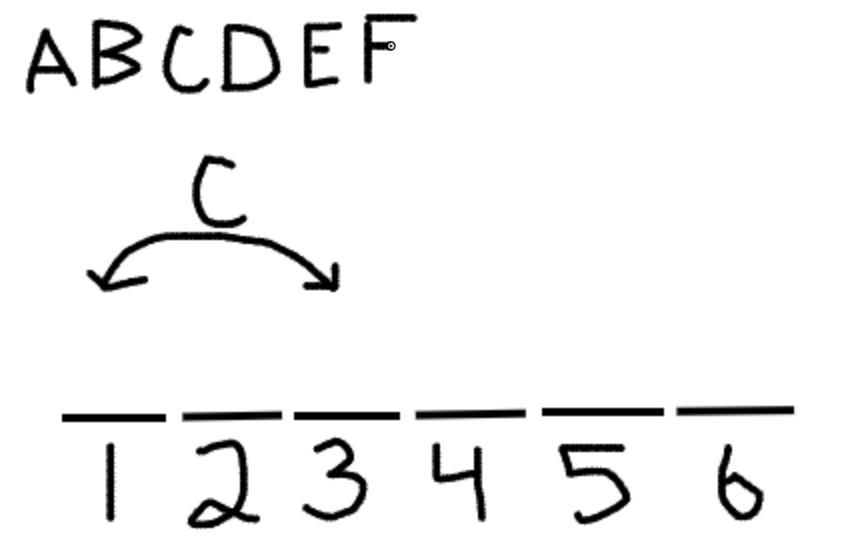
This is where it gets very important not to draw the rules in a way that’s going to leave you confused and scrambling to figure out what you meant by your own drawings. But assuming you represent the rules in your diagram in a way that makes sense to you, it’ll be extremely helpful and efficient going forward. And remember: if a rule can be drawn in your main diagram, then you should also draw it in any sub-diagrams you make for specific questions, unless the question proposes a change to that initial rule. 

Another guideline for what rules to put into your main diagram is any rule that tells you where an element cannot go. For example, if a rule specified that Danton could not be the fifth stop, you would draw that rule into your diagram like this.

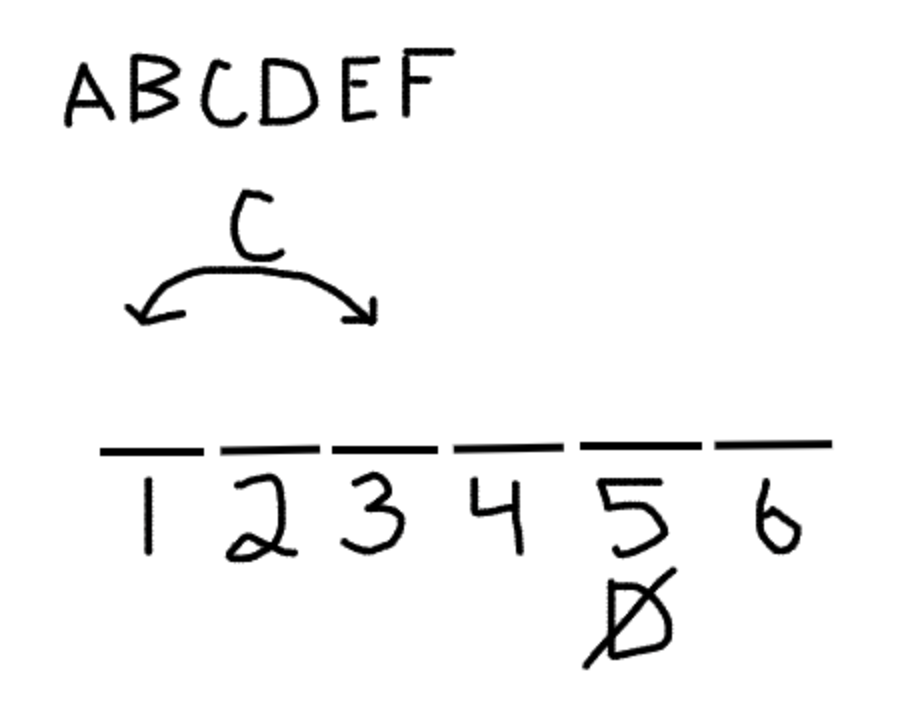
Another slightly more complicated rule that can go into your diagram is one that tells you about a range of slots a particular variable cannot go in. For example, let’s say a rule tells you that Brownsville cannot come any earlier than the fourth stop. This means B cannot go in slots 1-3. That’s simple enough to add to your diagram, like so:

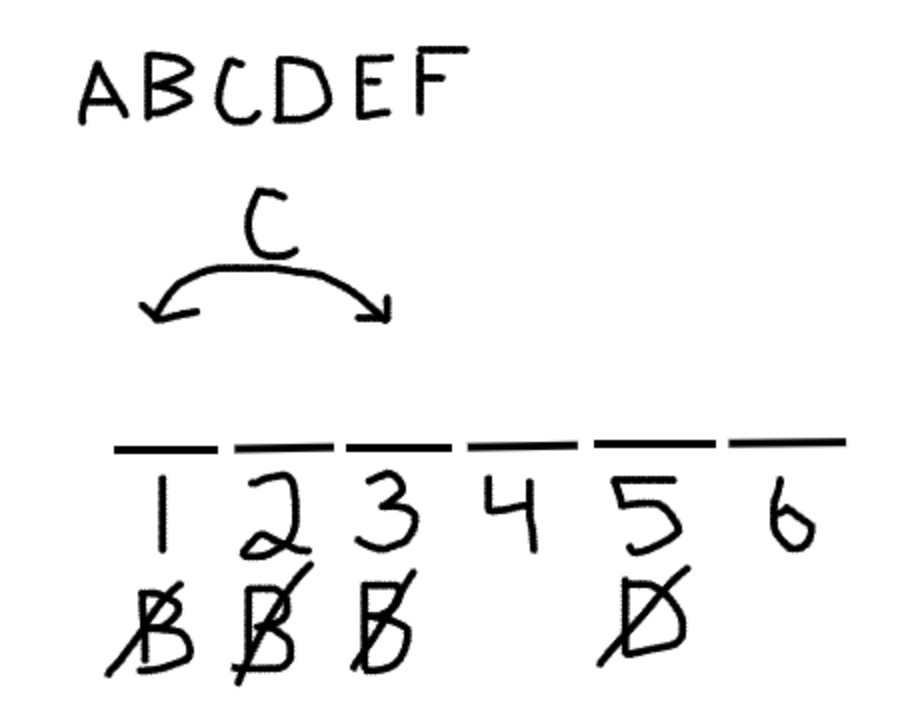
Adding these rules to your diagram actually helps you as you start to work through the questions, because it gives you a lot of visual information to help make it clear where certain things can and cannot go. This will make it far easier to avoid mistakes compared to keeping all those rules in your head. 

Combine Rules Wherever You Can

One of the most powerful things you can do in an ordering game is combine whatever rules you can. This will lead to information that’s both more powerful and more efficient. It’s easier to deal with one single rule than with several. It will also make your diagram more effective as an aid for dealing with the questions. 

The basic guideline for figuring out whether and how you can combine rules is to look for any variables that occur in more than one rule. If a variable occurs in more than one rule, that means you have information about its relationship to at least two other variables—which means you also now have information about those two (or more) other variables’ relationships with each other. 

Let’s look back over our initial rules.

The bus stops in Brownsville after stopping in Clarkmore.

The bus stops in Farm City after stopping in Danton.

The Danton stop comes exactly three stops after the stop in Ableton.

The Clarkmore stop is either first or third. 

We’ve already implemented the fourth rule into our main diagram, and we’ve demonstrated how to write the first three rules in the space above our diagram. But you can see that Danton occurs in both the second and the third rule. That means it’s probable that we can combine these rules for greater efficiency and information power. If we know that Ableton comes three stops before Danton, and Danton comes before Farm City, that also means Ableton must come before Farm City. Here’s how you can combine these rules into one super-rule:

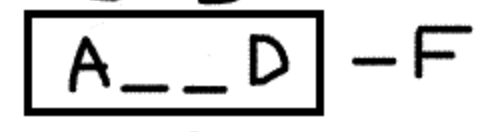
This has the double benefit of reducing the total number of rules you have to represent and remember, and it also makes the rules you’ve represented more effective and powerful. As long as you can combine rules in a way that you can understand, you’re likely to help yourself work more accurately and efficiently as you set about answering the questions and trying to fill in your diagram. 

There are some other ways you’ll want to combine rules in ordering games, and the trick with them is to capture the relevant information in a way that helps rather than confuses you.

Let’s say we had the following set of rules:

M comes after L.

J comes after N.

L comes before J. 

There are two different variables here that are represented more than once: L and J. That means we should be able to combine all these rules in a way that puts all four of the variables mentioned in relationship with each other. Here’s how we do that:

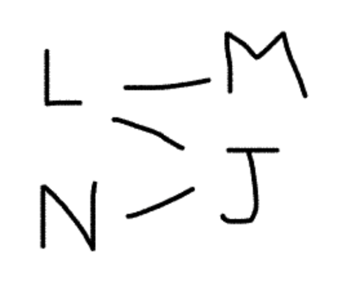
This reduces our three rules to one. Note that we are careful to position M and J directly on top of each other, just like L and N. This is because we don’t actually know whether M comes before or after J. Similarly, we don’t actually know whether L comes before N. 

Okay, now we’ve done just about everything we can to translate the prompt into visually represented rules and a clear diagram. Let’s revisit the entire prompt and then take a look at our diagram with all the pieces put together.

A bus driver is set to stop at six destinations—Ableton, Brownsville, Clarkmore, Danton, Edwardia, and Farm City. The bus only stops at each destination once.

The bus stops in Brownsville after stopping in Clarkmore.

The bus stops in Farm City after stopping in Danton.

The Danton stop comes exactly three stops after the stop in Ableton.

The Clarkmore stop is either first or third.

And here’s our main diagram, with all that information translated to a visual form:

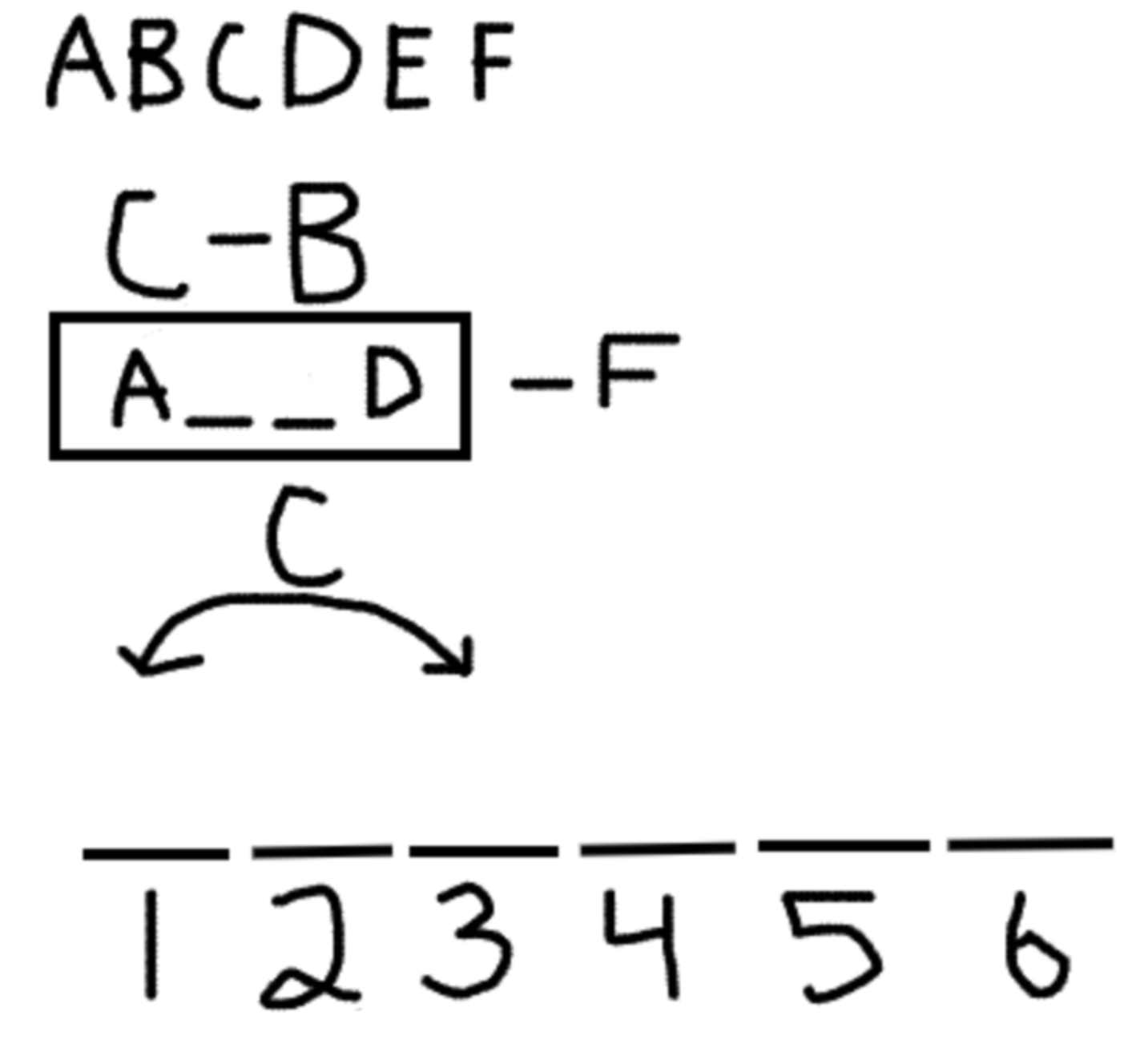
Pretty tidy, right? This combines all that abstract verbal information into a pretty digestible visual. Keep this as your main diagram, and then as you draw sub-diagrams for the specific questions associated with this particular game, you can re-draw the diagram. Re-drawing the diagram shouldn’t take too long and it’s helpful, because it keeps you from cluttering up your main diagram with information that only applies to one of the questions.

Conclusion

This one example should contain most of the techniques you’ll need to rely on in order to tackle just about any standard ordering game. And that’s saying a lot, because ordering games are the most basic and common of the LSAT logic games. And remember, if you’re really wanting to supercharge your LSAT logic games performance, consider online LSAT tutoring. Working with an expert LSAT tutor is the best thing you can do to maximize your performance, not only on LSAT logic games but on the entire LSAT. A qualified LSAT logic games tutor like the kind we have at MyGuru will help you develop a personally tailored approach that’s sure to deliver the best possible results on test day.